研究应力扰动下的断层摩擦滑动性质有助于准确评估水力压裂等工业注采行为对断层活动性的影响。前人使用单矿物断层泥在室温干燥条件下开展了大量应力扰动实验。但是，若要进一步将实验和理论工作外推至野外应用，还需要明确地下原位温压条件下应力扰动对天然断层泥摩擦滑动行为的影响并实现定量表征。为填补这一空白，本研究选择在荷兰乌得勒支大学旋转剪切摩擦实验系统上开展正应力扰动实验。断层泥样品来自四川盆地长宁页岩气田主要储层（龙马溪组页岩）及其附近一系列地层。所有实验在每一层位对应的原位温度压力条件下开展，并对样品施加不同振幅和频率的正应力扰动，以及不同剪切滑动速率（图1），最终使用考虑正应力变化的“速度-状态”摩擦本构模型（Linker和Dieterich, 1992，这里称之为“LD92模型”）以及基于摩擦滑动微观物理过程的CNS（Chen-Niemeijer-Spiers）模型（Niemeijer和Spiers, 2007; Chen和Spiers, 2016; Yu et al., 2024）对典型实验结果进行模拟。主要结论如下：

1）大部分样品在原位地质条件下具有速度强化性质，高频和高振幅正应力扰动会使此类断层泥的平均剪切强度发生明显弱化。剪应力的震荡幅度随扰动频率增加而降低，但是随扰动振幅的增加而增加（图2）；

2）正应力扰动期间，随着背景加载速率的增加，速度强化断层泥剪应力震荡幅度增加，然而断层泥平均剪切强度降低（图2）；

3）所有速度强化的断层泥在正应力扰动下展现出同样的摩擦滑动行为。说明在速度强化域内，断层泥矿物成分，背景温压条件并不是影响正应力扰动下断层摩擦滑动性质的重要因素（图3）；

4）LD92模型和CNS模型均可重现中低应力变化率下的剪切强度演化。但是高应力变化率下CNS模型的模拟结果与实验数据趋势更加接近（图4）。

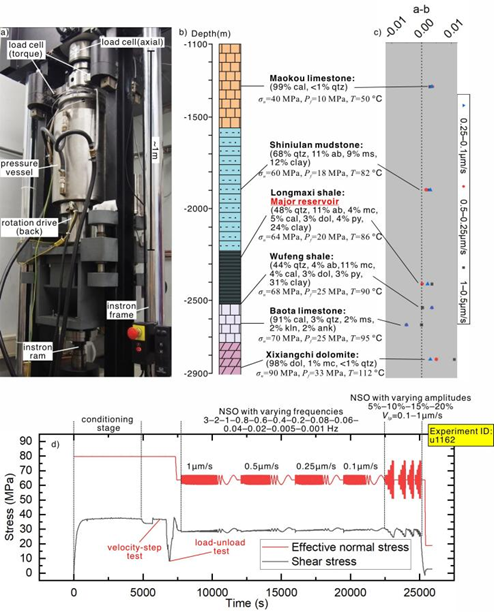
图1 （a）荷兰乌得勒支大学水热条件旋转剪切摩擦实验系统；（b）简化后的四川长宁页岩气田地层柱状图；

（c）各类样品“速度-状态”摩擦本构参数“a-b”值分布；（d）实验流程

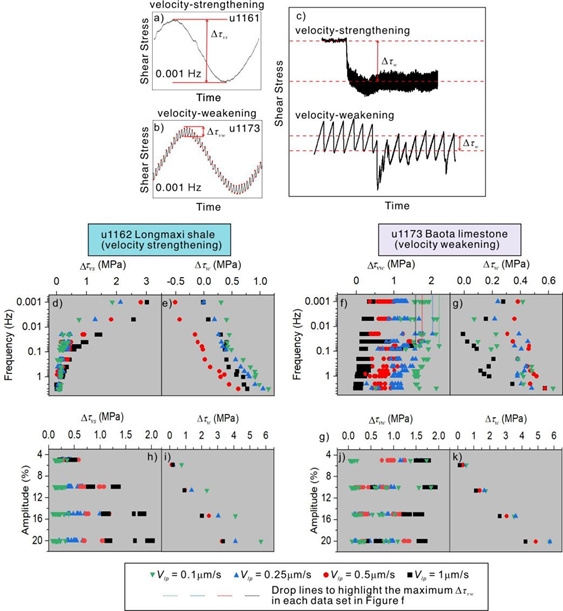
图2 扰动频率、扰动振幅及加载点速度对龙马溪组页岩和宝塔组石灰岩摩擦性质的影响。

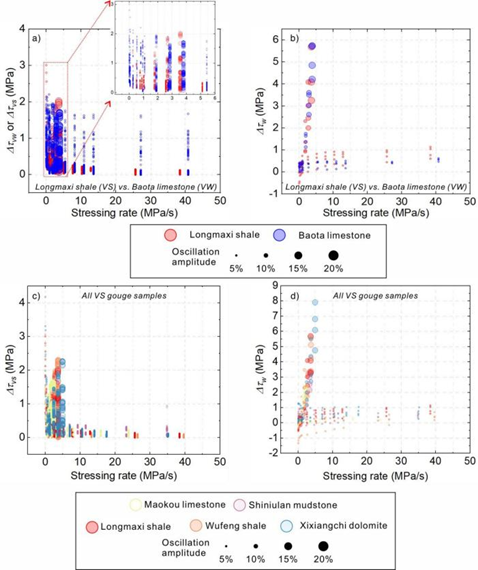
图3 应力加载速率（扰动频率与扰动的乘积）对实验结果的影响。（a）与（b）分别展示的是速度强化（龙马溪页岩）与速度弱化断层泥

（宝塔组石灰岩）剪应力震荡幅度、剪切强度弱化程度与应力加载速率之间的关系；（c）与（d）分别展示所有速度强化样品的剪应力震荡幅度、

剪切强度弱化程度与应力加载速率之间的关系

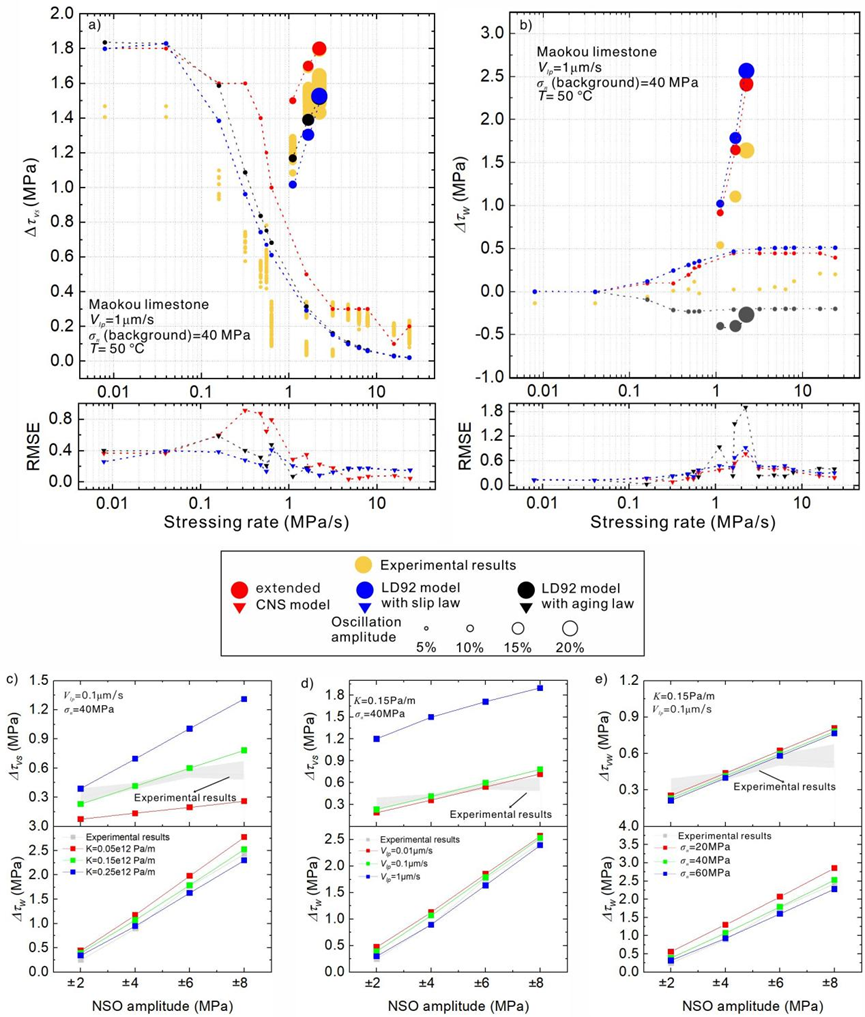
图4 基于CNS 模型和 LD92 模型模拟出的（a）剪应力震荡幅度和 (b) 平均剪切强度弱化程度 与应力加载速率之间的关系，

通过均方根误差（RMSE）评估模拟结果与实验数据之间的差异，黄色散点表示相同边界条件下的实验数据。

（c）-（e)分别展示了断层加载系统刚度、加载点速度以及背景正应力的参数敏感性分析结果

上述研究成果以“Effects of Periodic Normal Stress Oscillations on Frictional Properties of Simulated Natural Fault Gouges Under In Situ P‐T Conditions”为题，于2025年4月发表于Geophysical Research Letters（GRL）上，第一作者为中国地震局地质研究所构造物理研究室博士研究生余博文（现就职于东北石油大学地球科学学院与多资源协同陆相页岩油绿色开采全国重点实验室）。共同作者包括荷兰乌得勒支大学André Niemeijer助理教授与Hans de Bresser教授，构造物理研究室陈建业研究员、马胜利研究员以及博士研究生冯嘉辉（现就职于中国铁道科学研究院集团有限公司铁道科学技术研究发展中心）。本研究受国家自然科学基金（U1839211，U2239204，42174224）的联合资助。

原文信息：

Yu, B., Niemeijer, A. R., Chen, J., Ma, S., de Bresser, J. H. P., & Feng, J. (2025). Effects of periodic normal stress oscillations on frictional properties of simulated natural fault gouges under in situ P-T conditions. Geophysical Research Letters, 52, e2024GL112199. https://doi.org/10.1029/2024GL112199

参考文献：

[1] Chen, J., & Spiers, C. (2016). Rate and state frictional and healing behavior of carbonate fault gouge explained using microphysical model: Microphysical model for friction. Journal of Geophysical Research: Solid Earth, 121(12), 8642–8665. https://doi.org/10.1002/2016JB013470

[2] Linker, M. F., & Dieterich, J. H. (1992). Effects of variable normal stress on rock friction: Observations and constitutive equations. Journal of Geophysical Research, 97(B4), 4923–4940. https://doi.org/10.1029/92JB00017

[3] Niemeijer, A. R., & Spiers, C. J. (2007). A microphysical model for strong velocity weakening in phyllosilicate‐bearing fault gouges. Journal of Geophysical Research, 112(B10), B10405. https://doi.org/10.1029/2007JB005008

[4] Yu, B., Chen, J., Spiers, C. J., Ma, S., Zhang, M., Qi, W., & Chen, H. (2024). Frictional properties of simulated fault gouges subject to normal stress oscillation and implications for induced seismicity. Journal of Geophysical Research: Solid Earth, 129(9), e2024JB029521. https://doi.org/10.1029/2024JB029521