在一定的构造和气候条件下，每条河流都有一个理想的稳态高程剖面。在这个理想剖面上，河道每个点的侵蚀速率与构造抬升速率一致，因此河道能保持稳定。当某个分水岭两侧河道的稳态高程不一致时，则表明该分水岭处于不稳定的状态。分水岭将发生迁移从而达到稳态，即稳态高程较低的一侧将向稳态高程较高的一侧迁移（图1）。这意味着当分水岭两侧的河道源头点的稳态高程差（Δz_s）为0时，分水岭到达平衡状态（图1）。侵蚀速率是衡量分水岭迁移的重要指标。分水岭总是向侵蚀速率较低的一侧迁移。因此，探索Δz_s与侵蚀速率之间的联系可能对理解分水岭迁移机制具有重要意义。然而，Δzs如何造成跨分水岭的侵蚀速率差、并进一步造成分水岭迁移的，仍然是一个悬而未决的问题。

通过公式推导、数值模拟和实例分析，中国地震局地质研究所的叶轶佳博士、周朝助理研究员、卞爽助理研究员、石峰副研究员和中国科学院成都山地所的谭锡斌研究员和刘一多研究员组成的研究团队对上述科学问题进行了深入研究。研究团队首先推导了计算Δz_s的方程，量化了侵蚀系数、抬升速率、基准面、山脉宽度等不同因素对Δz_s的影响（图2）。在这个基础上，研究团队利用地貌演化的数值模拟（图3）以及两个自然实例（五台山和系舟山，图4），对分水岭迁移过程中Δz_s、侵蚀速率以及分水岭迁移速率之间的关系进行了探讨，并分析了分水岭迁移过程中Δz_s的吸收体（图3-5）。研究主要得到以下几点认识：

（1）在大多情况下，分水岭不稳定时跨分水岭的稳态高程差由山坡（hillslope）和河道（river channel）共同吸收。因此本研究建议同时使用Gilbert metrics和χ-plot方法来获得更为可靠的分水岭稳定性结果。当其中一种方法显示分水岭为不稳定时，即使另一种方法产生稳定的结果，我们也应该认为分水岭是不稳定的。

（2）当分水岭迁移时，扩张侧的侵蚀速率大于抬升速率，萎缩侧的侵蚀速率小于抬升速率。因此，不稳定的分水岭将对根据河道提取抬升历史信息造成一定的干扰。

（3）构造气候扰动将造成原本稳定的分水岭失去稳定状态，从而产生了跨分水岭的稳定高程差，进一步造成了跨分水岭的侵蚀速率差，分水岭开始朝向稳态迁移。在迁移过程中，上述参数逐渐减小（图6）。当构造、气候、岩性等因素保持较长时间（往往是一千万年以上，甚至一亿年以上）的稳定，分水岭才能达到新的稳态。因此，跨分水岭的稳态高程差是链接构造、气候扰动和分水岭迁移之间的重要桥梁，也是分水岭量化研究的重要参数。

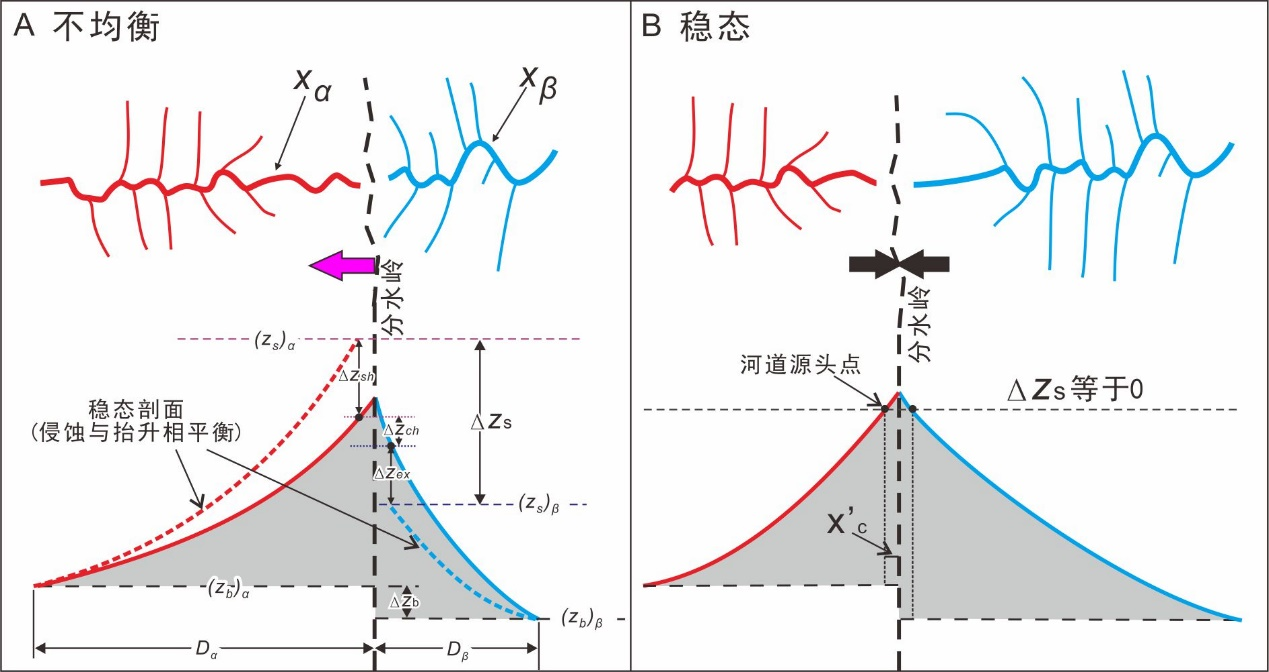
图1分水岭不稳定和稳定状态下的稳态高程差（Δz_s）示意图。（A）不稳定状态。（B）稳定状态。红色以及蓝色曲线代表分水岭两侧的河道。黑色虚线表示了流域分水岭。蓝色虚线以及红色虚线为理想的稳定状态下的高程剖面（侵蚀与抬升相平衡）。

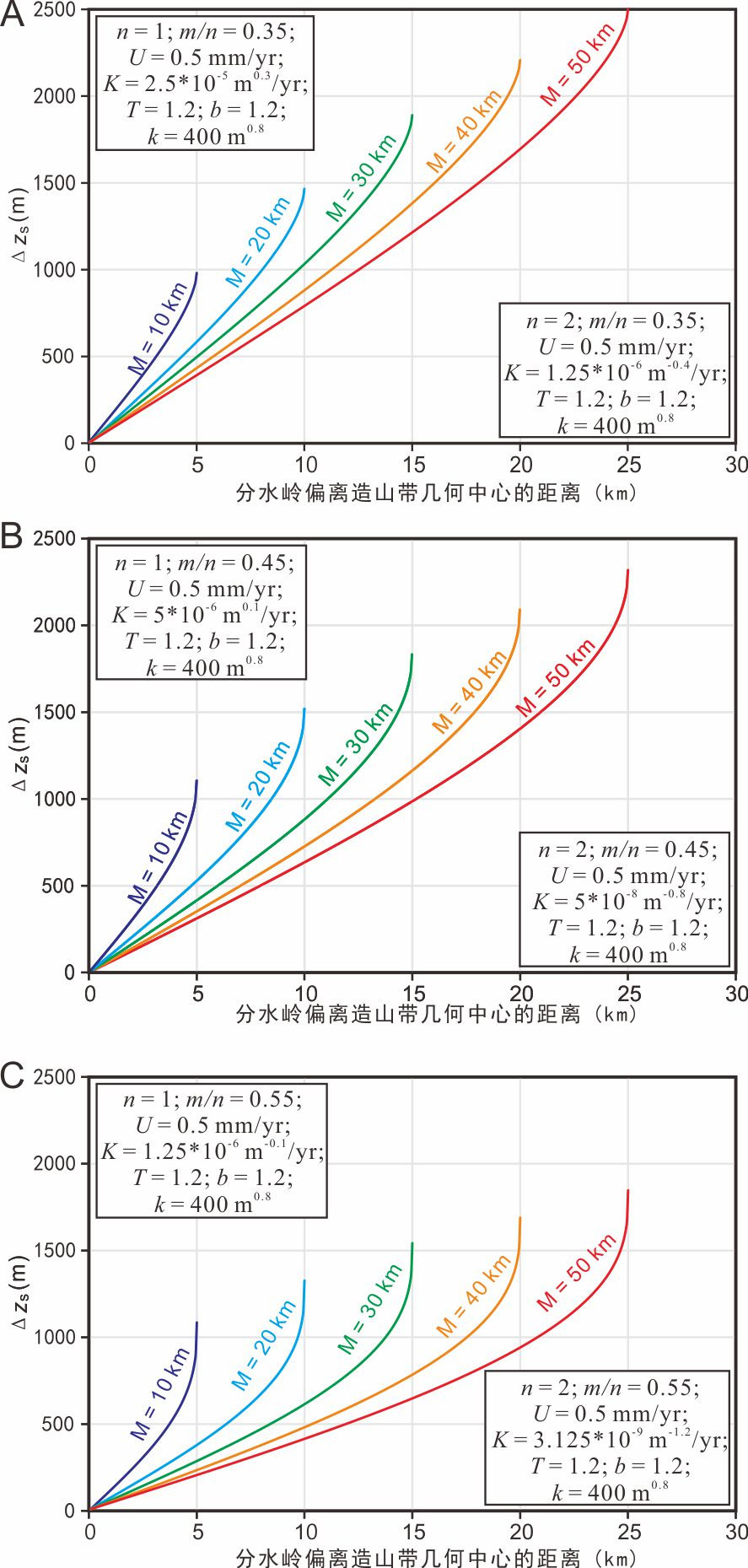
图2 造山带中Δz_s与分水岭偏离其稳定位置的距离之间的关系。（A）m/n = 0.35。（B）m/n = 0.45。（C）m/n = 0.55。M是分水岭垂直方向上的造山带的宽度。内置的正方形为用于计算Δz_s的相关参数。在每个图表中，不同的参数组合形成相同的曲线。

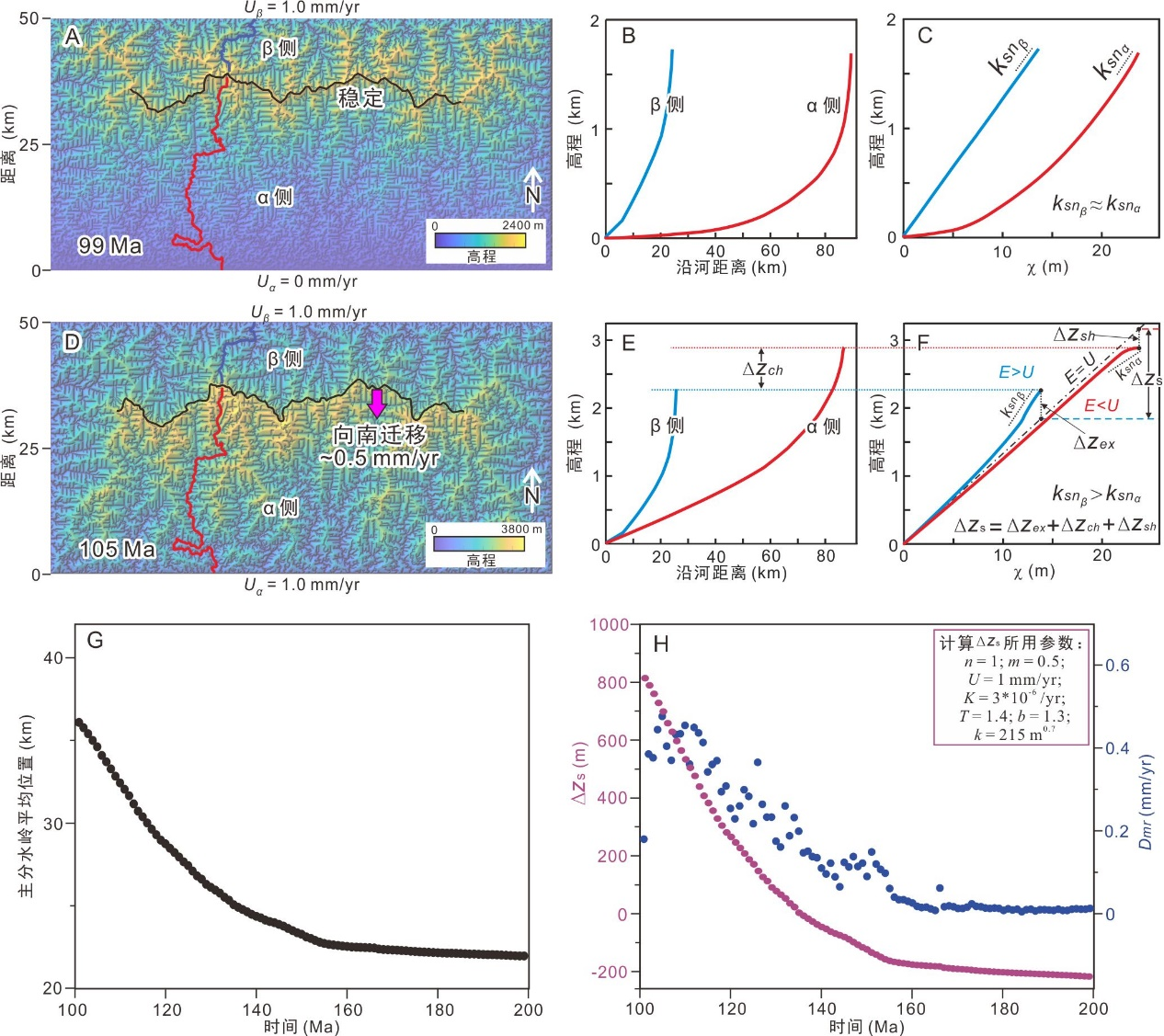
图3数值模拟结果及相关参数。（A）99 Ma的地形图。（B）99 Ma时两条河道的高程剖面图。（C）99 Ma时两条河道的χ-plot图。虽然χ值不同，但χ-plot最顶部的斜率是一样的，即ksn𝛼 ≈ ksnβ。（D）105 Ma的地形图。（E）105 Ma时两条河道的高程剖面图。（F）105 Ma时两条河道的χ-plot图。虚线表示其稳态剖面（侵蚀等于抬升）。（G）100-200 Ma间，主分水岭的平均位置。（H）基于数值模拟结果，根据分水岭位置计算的Δz_s（紫色圆点）以及分水岭迁移速率（蓝色圆点）。

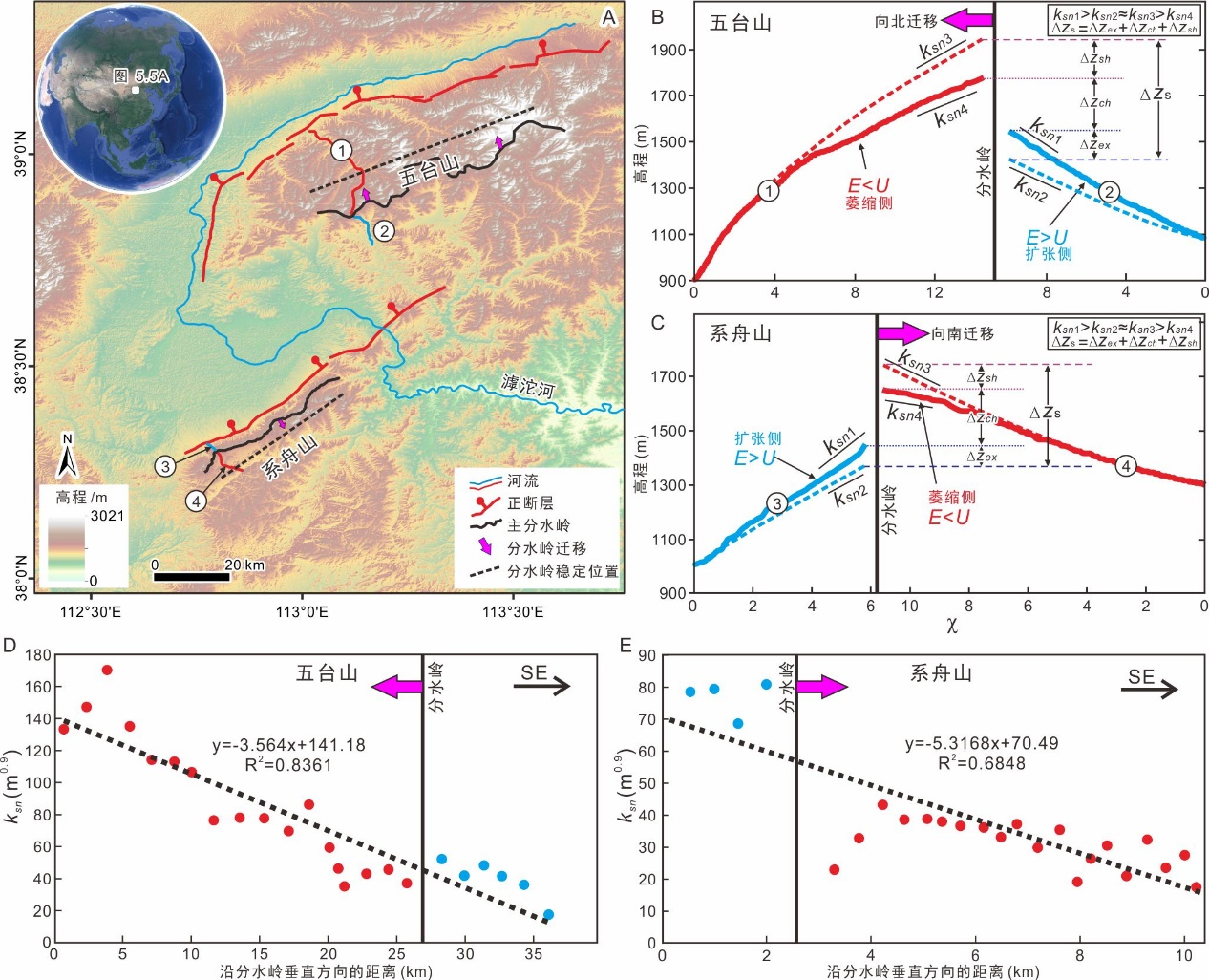
图 4 χ-plot及其稳态剖面。（A）区域地形图。五台山分水岭向北迁移，系舟山分水岭向南迁移。（B）五台山的χ-plots和稳态剖面示意图，具体位置见图5.5A。（C）系舟山χ-plots和稳态剖面示意图，具体位置见图5.5A。B、C图中的实线为五台山和系舟山χ-plot，虚线则代表其稳态剖面。红色代表萎缩一侧，蓝色代表扩张一侧。（D-E）ksn与距离的线性拟合。

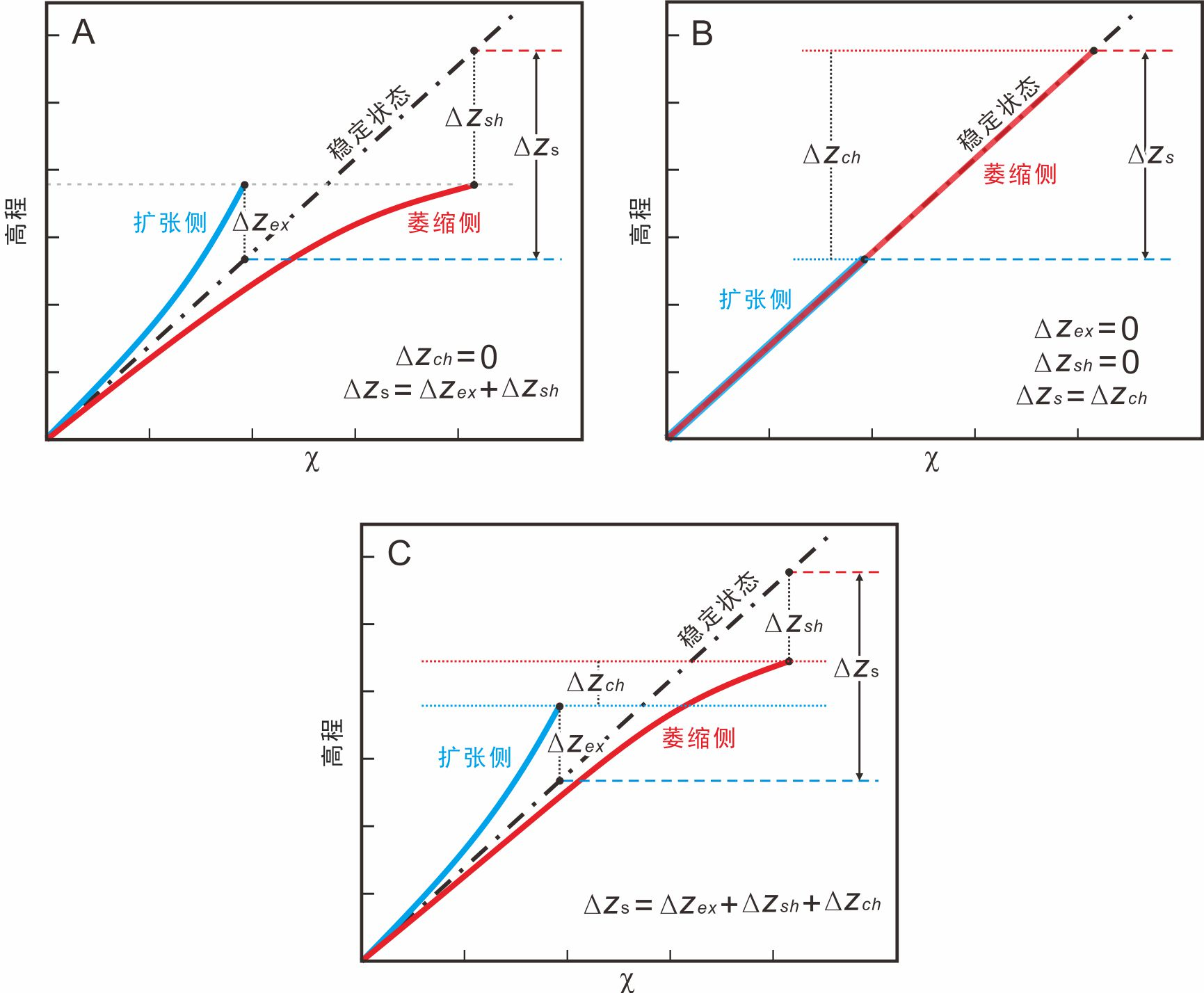
图 5 Δz_s吸收体的三种不同模型。（A&B）Δz_s吸收体的两种端元模型。在第一个端元模型中（A），Δz_s完全由河道所吸收。这种情况下，河道源头点具有相同的高程，意味着坡面对Δz_s的贡献不大。在第二个端元模型中（B），Δz_s完全由坡面的坡度所吸收，表现为分水岭两侧的河道源头点的高程不一样，存在高程差。（C）通用模型。Δz_s可以被河道以及源头山坡按不同比例所吸收。

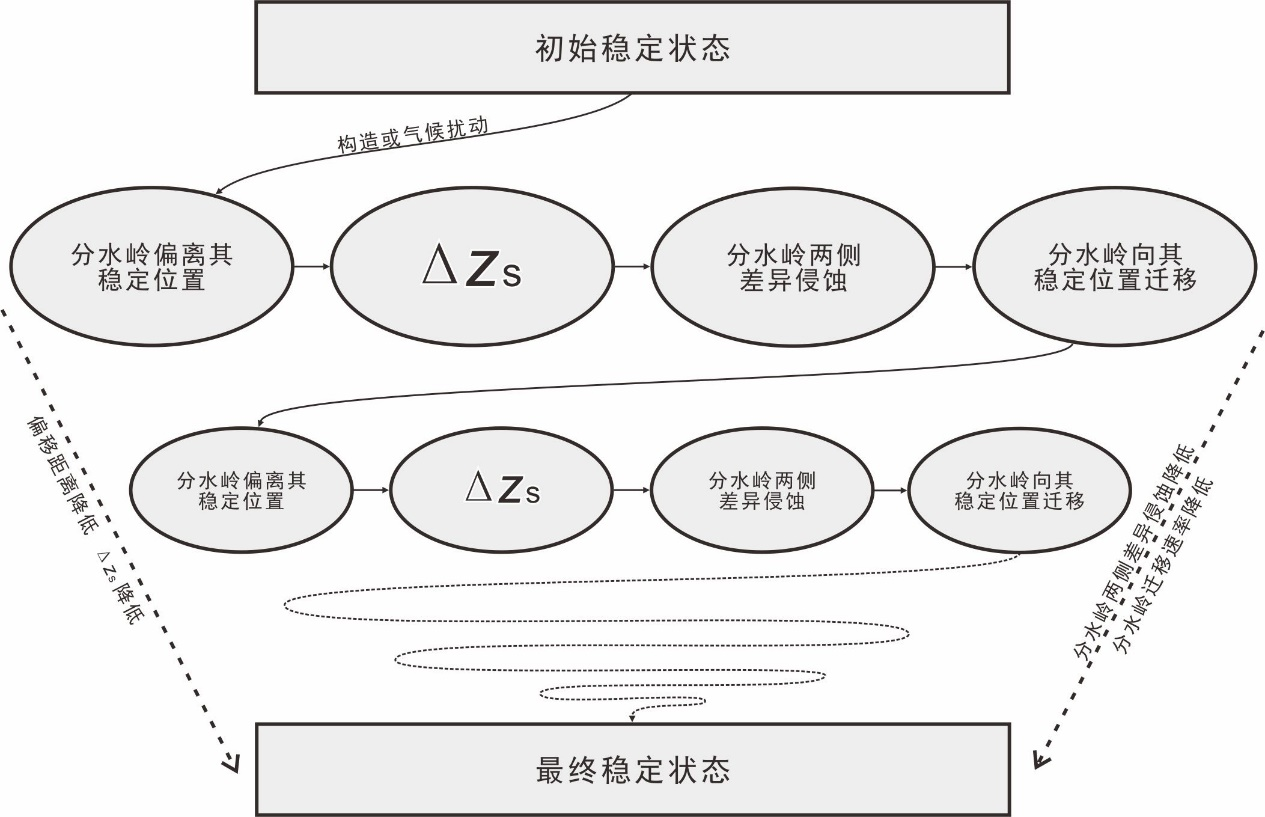
图 6 分水岭从不稳定到稳定状态的指标变化图。当分水岭偏离其稳定位置时，就会存在Δz_s。Δz_s导致分水岭两侧存在侵蚀速率差，从而推动分水岭向其稳定位置迁移。在分水岭的迁移过程中，分水岭偏离其稳定位置的水平距离逐渐减小。相应的，Δz_s以及迁移速率随着分水岭迁移也逐渐减小。构造、气候保持不变的情况下，这一过程将持续到分水岭达到新的稳定状态。

本研究促进了对分水岭迁移机制的理解，提出了分水岭稳定性判断的新标准，并首次计算了自然界中的跨分水岭稳态高程差（图4：五台山约600米，系舟山约400米）。研究得到了中国科学院百人计划项目(E2K2010010)资助。相关文章于2024年6月发表于《Earth Surface Processes and Landforms》杂志：Ye, Y., Tan, X.*, Zhou, C., Bian, S., Liu, Y. & Shi, F. (2024) Cross-divide difference in channel-head steady-state elevation controls drainage-divide migration. Earth Surface Processes and Landforms, 1–12.